量子散逸系の半古典シミュレーション
励起エネルギー移動や電荷移動のダイナミクスを量子力学的に考えるためには、 分子環境からの影響を考慮した量子解放系の問題として取り扱う必要があります。 サーフェスホッピング法や エーレンフェスト動力学法は、電子状態の時間発展をシュレーディンガー方程式で、 核の運動をニュートン方程式で取り扱うことによって、 電子状態間の非断熱遷移過程をシミュレーションする方法として有名で良く用いられます。 しかし、電子状態間のデコヒーレンス効果の欠如やボルツマン平衡に収束しないなどの問題が存在し、 精度を上げるためにアドホックな補正を加える必要があります。
CottonとMillerが開発したSymmetrical quasi-classical (SQC)法は、
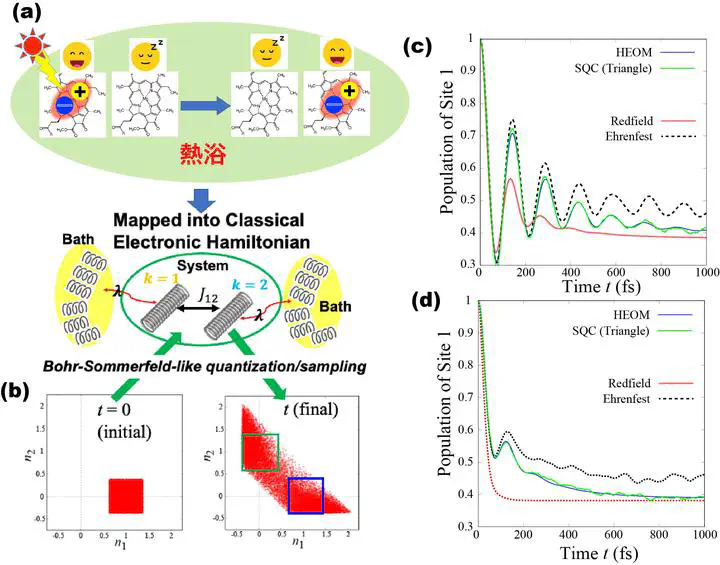
- 図(a): 離散的なN電子状態の自由度を、 N個の単一励起調和振動子の連続的な正準変数に射影することで、 核の自由度も合わせた古典振電ハミルトニアンを構築し、 正準運動方程式に従って古典的に時間発展させる(Meyer-Miller-Stock-Thoss マッピング法)
- 図(b):Bohr-Sommerfeld量子化に習って、量子状態の初期条件から、 作用・角変数の位相空間上で整数/半整数量子数を中心に、 縮小したゼロ点エネルギー(γ)の幅をもつビン(窓関数)で初期アンサンブルを発生させ、 古典で時間発展させた後に、同じく作用・角変数位相空間上で窓関数を用いて 連続正準変数を量子化する(対称的窓関数サンプリング)
という手順で、非断熱遷移過程が古典分子動力学シミュレーションのような形で実行されます。
我々は、エネルギー散逸を引き起こす熱浴と結合した量子解放系の問題について、 SQC法を用いた研究を行っています。 図(c)(d)では、Debye型スペクトル関数を持つ熱浴に結合した二状態サイトエキシトンモデルの に対して、ベンチマーク計算を行った結果をプロットしています。 SQC法シミュレーションが正確な階層型量子散逸系運動方程式(HEOM)の結果を 良く再現している事がわかります。