Quasi-classical Mapping Hamiltonian Dynamics Simulation of Quantum Dissipative Systems

To describe the dynamics of excitation energy transfer and charge transfer quantum-mechanically, it is necessary to treat these processes as quantum open system problems because the effects of the molecular environment play a crucial role.

Commonly used methods such as the surface hopping and Ehrenfest dynamics approaches simulate nonadiabatic transitions between electronic states by evolving the electronic states using the Schrödinger equation while treating nuclear motion classically via Newton’s equations. However, these methods face challenges — such as insufficient treatment of decoherence effects between electronic states and failure to converge to Boltzmann equilibrium — requiring ad hoc corrections to improve accuracy.

As an alternative promising approach, we employ the Symmetrical Quasi-Classical (SQC) method developed by Cotton and Miller:

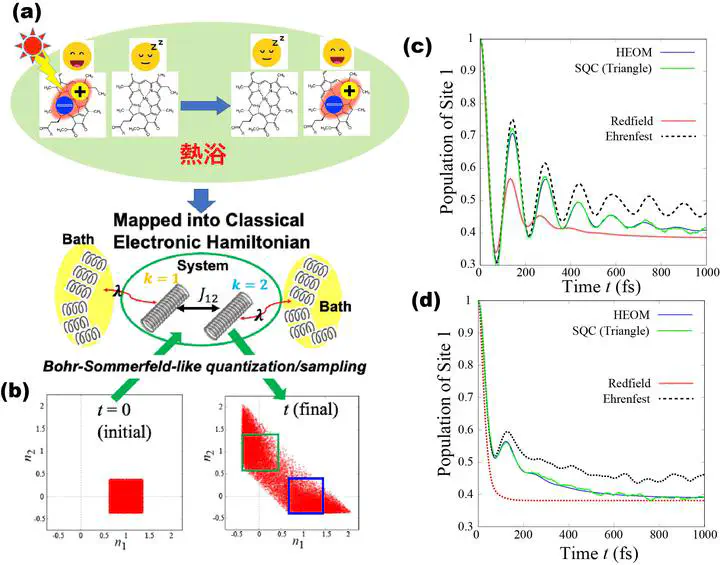
• Figure (a): In this approach, the degrees of freedom of N discrete electronic states are mapped onto continuous canonical variables of N singly excited harmonic oscillators, constructing a classical vibronic Hamiltonian that includes both electronic and nuclear degrees of freedom. This is called Meyer-Miller-Stock-Thoss mapping. The time evolution of the mapping variables is then simulated using classical canonical equations of motion on the continuous phase space.
• Figure (b): Following Bohr-Sommerfeld quantization, an initial ensemble is generated by sampling quantum state initial conditions within an action-angle phase-space bin (window function) centered at integer or half-integer quantum numbers, with a width defined by the reduced zero-point energy (γ). After classical time evolution, the continuous variables are quantized using a symmetric window function in phase space.

This enables the simulation of nonadiabatic transition processes analogous to classical molecular dynamics but incorporating essential quantum effects. We are applying the SQC method to investigate quantum open systems coupled to thermal baths, which induce energy dissipation. Figures (c) and (d): These plots show benchmark results for a two-state site-exciton model coupled to a thermal bath characterized by a Debye-type spectral density. The simulations demonstrate that the SQC method successfully reproduces the results of highly accurate hierarchical equations of motion (HEOM) for quantum dissipative systems, confirming the validity and reliability of this approach.

We are also using the quasi-classical mapping dynamics methods newly developed by Richardson et al., including modified linearized semi-classical (mLSC) and spin-mapping (SM). We have applied these quasi-classical mapping Hamiltonian dynamics methods to study photosynthesis, singlet fission, and quantum decision-making.